
Le premier exemple est tout simplement [5,7
11,13].
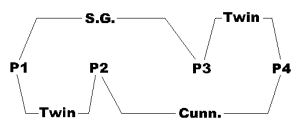
Ces groupes de nombres premiers que j'appelle "BiTwins"
sont assez faciles à trouver (et sont mêmes un peu esthétiques
!). En effet, à cause de leur liaisons deux à deux, les
nombres constituants ont des formes linéaires simples. Un petit calcul
montre que p1 est de la forme 30a-1 (pour p1>5), p2 = 30a+1, p3 = 60a-1,
p4 = 60a+1. En base décimale ils ont donc une terminaison en 9 et
1 uniquement (twin).
On trouve immédiatement les quelques suivants
:
[29,31 59,61] [659,661
1319,1321] [809,811 1619,1621]
[2129,2131 4259,4261] ... ...
... [2003999,2004001 4007999,4008001] ... ...
Généralisation :
Il est possible de poursuivre le processus pour obtenir une chaîne
de plusieurs "BiTwins" (et peut-être aussi longue que l'on veut), selon
le schéma ci-dessous :
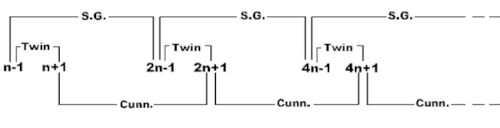
On notera que l'on obtient des chaînes de Cunningham de première et de seconde espèce de longueur = nombre de maillons+1. Les calculs sont toujours aussi simples car les formes linéaires deviennent pour n 210*a (pour 2 maillons ) 2310*a+0,420,1890 (pour 3 maillons) etc. ....
Pour 2 maillons le plus petit est : [211049,211051 422099,422101 844199,844201]
Pour 3 maillons le plus petit est : [253679,253681 507359,507361 1014719,1014721 2029439,2029441]
....
Des questions se posent :
- a (de 30*a) est-il facilement décomposable en facteurs premiers
pour n grand ?
- p2 peut-il se mettre sous la forme k*2m+1 pour pouvoir utiliser
le théorème de Proth ? . J'ai pu vérifier que cela
est possible, mais malheureusement rarement (10 fois pour
n<6*1010):
| Rang | "BiTwins" k*2m+/-1 k*2m+1+/-1 |
| 1 | 855*210-1, 855*210+1 855*211-1, 855*211+1 |
| 2 | 5565*213-1, 5565*213+1 5565*214-1, 5565*214+1 |
| 3 | 4935*216-1, 4935*216+1 4935*217-1, 4935*217+1 |
| 4 | 6105*216-1, 6105*216+1 6105*217-1, 6105*217+1 |
| 5 | 735*220-1, 735*220+1 735*221-1, 735*221+1 |
| 6 | 31215*215-1, 31215*215+1 31215*216-1, 31215*216+1 |
| 7 | 47745*218-1, 47745*218+1 47745*219-1, 47745*219+1 |
| 8 | 80985*218-1, 80985*218+1 80985*219-1, 80985*219+1 |
| 9 | 50505*220-1, 50505*220+1 50505*221-1, 50505*221+1 |
| 10 | 54645*220-1, 54645*220+1 54645*221-1, 54645*221+1 |
| Voir les records |
- p2 peut-il se mettre sous la forme
p*2b3c5d+1 avec p premier, pour pouvoir
utiliser un test de primalité (n-1) plus général. C'est
aussi possible et les "BitWins" sont nettement moins rares ( 197 pour
n<107):
| Rang | "BiTwins" p*2b3c5d+-1 | p |
| 1 | 659,661 1319,1321 | 11 |
| 2 | 2129,2131 4259,4261 | 71 |
| 3 | 2549,2551 5099,5101 | 17 |
| 4 | 3329,3331 6659,6661 | 37 |
| 5 | 3389,3391 6779,6781 | 113 |
Il est même possible de trouver des "Bitwins" de cette forme avec p=1
(3 pour n<109):
| Rang | "BiTwins" 2b3c5d+-1 | "BiTwins" 2b3c5d+-1 |
| 1 | 29,31 59,61 | 2.3.5-1, 2.3.5+1 22.3.5-1, 22.3.5+1 |
| 2 | 809,811 1619,1621 | 2.34.5-1, 2.34.5+1 22.34.5-1, 22.34.5+1 |
| 3 | 431999999,432000001 863999999,864000001 | 210.33.56-1, 210.33.56+1 211.33.56-1, 211.33.56+1 |
Quelques autres résultats numériques :
| Rang | "BiTwins" 1 maillon |
| 1 | 5,7 11,13 |
| 2 | 29,31 59,61 |
| 3 | 659,661 1319,1321 |
| 4 | 809,811 1619,1621 |
| 5 | 2129,2131 4259,4261 |
| 6 | 2549,2551 5099,5101 |
| 7 | 3329,3331 6659,6661 |
| 8 | 3389,3391 6779,6781 |
| 9 | 5849,5851 11699,11701 |
| 10 | 6269,6271 12539,12541 |
| Voir les records |
| Rang | "BiTwins" 2 maillons |
| 1 | 211049,211051 422099,422101 844199,844201 |
| 2 | 248639,248641 497279,497281 994559,994561 |
| 3 | 253679,253681 507359,507361 1014719,1014721 |
| 4 | 410339,410341 820679,820681 1641359,1641361 |
| 5 | 507359,507361 1014719,1014721 2029439,2029441 |
| 6 | 605639,605641 1211279,1211281 2422559,2422561 |
| 7 | 1121189,1121191 2242379,2242381 4484759,4484761 |
| 8 | 1138829,1138831 2277659,2277661 4555319,4555321 |
| 9 | 1262099,1262101 2524199,2524201 5048399,5048401 |
| 10 | 2162579,2162581 4325159,4325161 8650319,8650321 |
| Voir les records |
| Rang | "BiTwins" 3 maillons |
| 1 | 253679,253681 507359,507361 1014719,1014721 2029439,2029441 |
| 2 | 1138829,1138831 2277659,2277661 4555319,4555321 9110639,9110641 |
| 3 | 58680929,58680931 117361859,117361861 234723719,234723721 469447439,469447441 |
| 4 | 90895769,90895771 181791539,181791541 363583079,363583081 727166159,727166161 |
| Voir les records |
| n<= | "BiTwins" 1 maillon |
"BiTwins" 2 maillons |
"BiTwins" 3 maillons |
| 10 | 1 | 0 | 0 |
| 102 | 2 | 0 | 0 |
| 103 | 4 | 0 | 0 |
| 104 | 10 | 0 | 0 |
| 105 | 29 | 0 | 0 |
| 106 | 144 | 6 | 1 |
| 107 | 752 | 15 | 2 |
| 108 | 4390 | 52 | 4 |
BiTwins généralisés :
Si l'on remplace les chaînes de Cunningham de première et de
seconde espèce respectivement par des chaînes
de Cunningham généralisés on peut obtenir des BiTwins
généralisés, selon le schéma ci-dessous :
