Le cryptage R.S.A.

Origine :

    Le premier algorithme de cryptage à clef publique a été développé par R. Merckle et M. Hellman en 1977. Il fut vite obsolète grâce aux travaux de Shamir, Zippel et Herlestman, de célèbres cryptanalyseurs.

    En 1978, l'algorithme à clé publique de Rivest, Shamir et Adelman (R.S.A.) apparaît. Il sert encore au début du XXI^ème siècle à protéger les codes nucléaires des armées américaines et soviétiques...

Mécanisme :

     L’algorithme du système R.S.A. peut se résumer à 5 étapes :

        1) Choisir deux grands nombres premiers p et q de plus de 80 chiffres (en dessous, le code est vulnérable)

        2) Calculer n=p.q et f=(p-1).(q-1)

        3) Choisir un nombre e premier avec f et n (i.e. tel que pgcd(e,f.n)=1)

        4) Trouver d tel que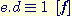

        5) Le message à crypter est converti en blocs de chiffres , tous inférieurs à n. Pour chiffrer le bloc , on calcule modulo n (les 2 paramètres de cryptage sont donc e et n).

    Pour déchiffrer le bloc 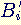, on calcule 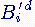modulo n (les 2 paramètres de décryptage sont donc n et d, et donc, à cause de la définition de d, on doit connaître f, donc p et q).

    Le chiffrement et le déchiffrement sont l’inverse l’un de l’autre. En effet :
    
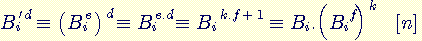
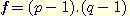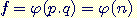Or, donc , où 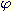est l'indicateur d'Euler. Par le théorème d'Euler, on a 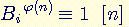donc 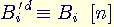. Comme , on a 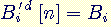, et on retrouve bien le message original.

    La clé publique est la paire (e, n) et la clé secrète est d, donc aussi p et q.

Conditions d'utilisation optimale du R.S.A. :

    Il faut savoir qu’un mauvais choix des paramètres p, q, d et e peut rendre le système relativement vulnérable. Pour cela, les concepteur du système ont proposé un certain nombre de règles :

    - Il faut choisir n = p.q de taille supérieure ou égale à 512 bits (155 chiffres décimaux environ).

    - Il faut prendre p et q de taille sensiblement égale, mais pas trop proches en valeur absolue.

    - Il faut choisir, si possible, des nombres premiers p et q, tels que p-1, p+1, q-1 et q+1 possèdent de grands facteurs premiers.

    La sécurité du système RSA se base sur le fait qu’il y a une impossibilité pratique de factoriser un grand nombre de quelques centaines de chiffres en un temps raisonnable : Selon R.S.A., factoriser un nombre à 200 chiffres demande 4 milliards d’années de calcul machine. Factoriser un nombre de 500 chiffres demande 10²⁵ ans. La robustesse du R.S.A. apparaît donc liée à la difficulté de la factorisation avec les méthodes actuelles.

    Pour « casser » un message chiffré par la méthode RSA, sachant qu’on ne sait pas calculer les racines e-ièmes modulo n de celui-ci, on s’attaquera à la méthode de détermination des clés. En l’examinant, on devine facilement comment forcer le codage : le choix des clés s’effectuant à partir de la formule e.d=K.f+1, on essaie de déterminer la clé secrète (d) à partir de la clé publique en résolvant l’équation. Pour la résoudre, il suffit d’avoir f. Pour obtenir f, il faut le décomposer en ses facteurs premiers p et q.

    Cependant, il n'a jamais été démontré que le code ne pouvait être cassé sans la connaissance de p et q !

Exemple 1:

     p = 3, q = 11, n = 3 x 11, f = (11–1).(3–1) = 20. On choisit d=7 (7 et 20 sont bien premiers entre eux).

    e = 3 car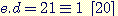

    On choisit un message, par exemple SUZANNE :

     Remarque : Bien sûr, il est fortement déconseillé de prendre des blocs d'une lettre auquel cas le R.S.A devient un cryptage de substitution !

Voir feuille de calcul Maple.