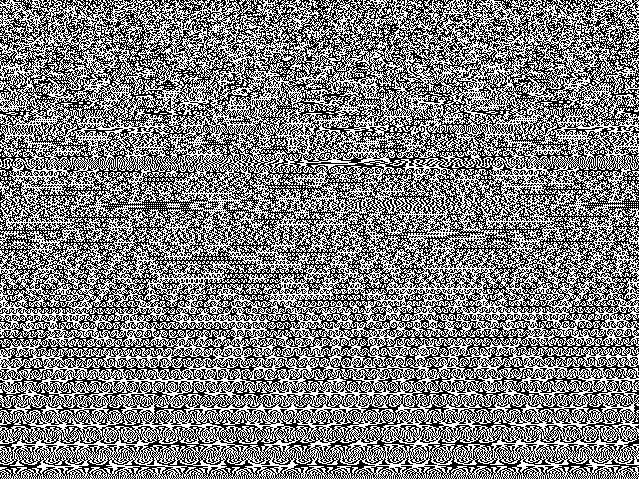
Let's take a big number, say N=1020. Let's do the following divisions : N/1, N/2, N/3, N/4, N/5 ...
Each time the quotient is even, we place a black pixel on the screen, each time it is odd, a white pixel. At the end of the first line, we pass to the next line and so on... At the end of the graph we must verify that the divisor is really under the number and even under his square root.
That's what we are like to obtain:
We notice on that strange graph that the beginning is quite chaotic and progressively sequences of little spirals are taking shape and grow quickly.
Why is this graph like this ? I don't have any answer yet. So, if you have an idea, please e-mail me !