Graph 1
Let the following polar function :
r(x)=
|
where x is in radians
I use this UBASIC program to draw this function :
5 cls:screen 23
7 input "Scale:";C
8 clr J
9 line (319,240)-(321,240):line (320,239)-(320,241)
10 for I=2 to 5000000
12 Prime=prmdiv(I)
13 if Prime=I inc J
15 if Prime=I then pset ((I*cos(I))/C+320,(I*sin(I))/C+240),1
17 if inkey="+" then cancel for:C=C/2:cls:goto 9
19 if inkey="-" then cancel for:C=C*2:cls:goto 9
20 next
That's what we have at different scales (when we go away from the center) :
Graph 1
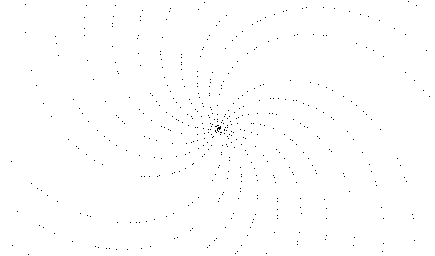Graph 2
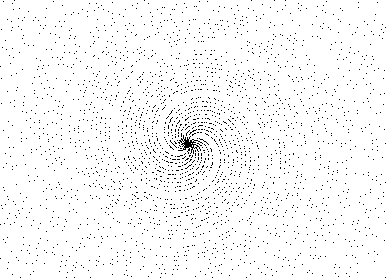Graph 3
At the beginning (Graph 1), we can only see 2 rotating arms in the spiral. But gradually (Graph 2 and 3), we can see 2 big arms in which we have exactly 10 little arms.Why 10 ? I never used this number neither in the function nor in the program. Now, if we take x in degrees, we obtain a simple Archimede spiral less and less dense (due to the prime numbers rarefaction). So, would it be an hidden property of pi ?
Thanks to :
- Isaac Keslassy (11 Apr 1999), who has found that it wasn't a property of pi but a property of a range including pi (3.141 to 3.144) : curious, no ?
- Douglas C. Sloan (02 Oct 1999), for his philosophical explanations.
- Erick Wong (03 Oct 1999), for his excellent explanations of all the phenomenas. Here are extracts from the mail:
The prime spiral on your web page is easily explained in terms of rational approximations to 2*Pi (this is why numbers close to Pi also work, since they have the same approximants).
The best rational approximations for 2*Pi, given by the continued fraction 6+1/(3+1/(1+1/(1+1/(7+1/(2+...))))) are 6/1, 19/3, 25/4, 44/7, 333/53, 710/113, ...
Now, imagine plotting the numbers (6n+1) in radians. We get the spiral instead of a straight line because 6 is not exactly 2*Pi.
The spirals are counterclockwise because 6 < 2*Pi radians.
I think that 19/3 and 25/4 are not close enough to 2*Pi to be recognized, and 44/7 is much better. Well, Phi(44)=20 and that's why there are 20 arms (the two large "gaps" correspond to the spirals 44n+{10,11,12} and 44n+{32,33,34}, which are never prime. Now the spirals are clockwise because 44>2*Pi*7.
As we zoom out further, I expect to find spirals corresponding to the very good approximation 710/113. and ther should be exactly Phi(710)=280 arms.
- Alan Powell (05 Oct 1999), for his good explanations about the rotation of the graph and the number of arms.
- Serge Boisse (07 Jan 2004), who has independently discovered the "prime spiral". See http://membres.lycos.fr/boisse/maths/primes_spiral.html for more information.