I call prime numbers in network a sequence of primes in arithmetic and/or geometric progression with more than one dimension.

This sequence can be made of consecutive primes.

"2D Primes":

For arithmetic progressions, the problem is to find primes with a gap g1 "horizontally" and g2 "vertically" :

The number at the top-left of tables indicates the number of primes, c indicates consecutive primes.

2D Twins :

2D Network :

   2D Staircase :

               

7c	2-->(Twins)
4 |  V	5	7
		11	13
			17	19
				23

  If g1=2 we also have Twins in arithmetic progression of difference g2 :

   

8c	10 -->
8 | V	67944073	67944083
		67944091	67944101
			67944109	67944119
				67944127	67944137

2D 4x2 :

8	6 -->
30 |	11	17	23	29
	41	47	53	59

 

8c	6 -->
20 |	344231	344237	344243	344249
	344251	344257	344263	344269

2D Triangular :

"3D Primes":

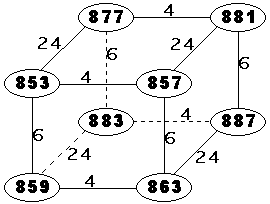
For arithmetic progressions, the problem is to find primes with a gap g1 "horizontally", g2 "vertically" and g3 "in depth".

Below, here is the smallest with 8 consecutive primes (g1=4,g2=6,g3=24) :

It is also possible to write them easily with symetric sequences of their differences, with the starting prime :

• "3D" : {13 ;4,2,4,14,4,2,4}
• "3D consecutive" : {853 ;4,2,4,14,4,2,4}
  
  

Primes in network and k-tuplets :

We have the possibility to transform them in particular k-tuplets, for example :

• "2D Triangular consecutive" : {4116419 + 0,24,30,48,54,60}
• "3D" : {13 + 0,4,6,10,24,28,30,34}
• "3D consecutive" : {853 + 0,4,6,10,24,28,30,34}
  

Twins in arithmetic progression (consecutive) :

If we consider the particular case g1=2, g2 increasing and the smallest p1,p2,p3 corresponding, we have 3 odd primes with the smallest gap (g1=2) and the biggest (g2). I call this triplet "quartered prime numbers".

A strange coincidence appeares often. For the ticked g2 (*), we rediscover the first occurence of prime gaps ! Would it have any sort of immediate compensation between a very small gap and a very large one ?

With 2 Twins :

With 3 Twins :

Challenges :

Find prime numbers in network (consecutive or not)

• The longest chain of twins (*)
• A 2D network with a maximum of primes
• A 3D network with a maximum of primes
• ......
  

(*) On Mai 13, 2000 Paul Jobling has found 12 sets of 10 twin primes in (not consecutive) arithmetic progression :

i=0 to 9
(7146+i*7087)*17#+239670 +- 1
(27193+i*15352)*17#+39930 +- 1
(103299+i*8702)*17#+409602 +- 1
(240056+i*1185)*17#+399000 +- 1
(28070+i*24909)*17#+369168 +- 1
(43711+i*33725)*17#+160878 +- 1
(392688+i*2040)*17#+429018 +- 1
(263377+i*18202)*17#+359172 +- 1
(1952+i*70022)*17#+392772 +- 1
(104521+i*62645)*17#+353532 +- 1
(189110+i*89957)*17#+244200 +- 1
(419358+i*62769)*17#+424980 +- 1

•  Prime k-tuplets  by Tony Forbes.
•  Yves Gallot's Proth.exe and Cunningham Chains  by Warut Roonguthai.