J'appelle nombres premiers en réseau une suite de nombres premiers composée de progressions arithmétiques et/ou géométriques sur plusieurs dimensions (2 ou plus).

Cette suite peut-être formée de nombres premiers consécutifs.

Nombres premiers "2D":

Pour des progressions arithmétiques il s'agit de trouver des nombres premiers avec un écart e1 "horizontalement"
et e2 "verticalement" :

Le nombre en haut à gauche des tableaux indique le nombre de nombres premiers, c indique qu'il s'agit de nombres premiers consécutifs.

2D Jumeaux :

2D Reseau :

   2D Escalier :

               

7c	2-->(jumeaux)
4 |  V	5	7
		11	13
			17	19
				23

  Si e1=2 on a aussi des jumeaux en progression arithmétique de raison e2 :

   

8c	10 -->
8 | V	67944073	67944083
		67944091	67944101
			67944109	67944119
				67944127	67944137

2D 4x2 :

8	6 -->
30 |	11	17	23	29
	41	47	53	59

 

8c	6 -->
20 |	344231	344237	344243	344249
	344251	344257	344263	344269

2D Triangle :

Nombres premiers "3D":

Pour des progressions arithmétiques il s'agit de trouver des nombres premiers avec un écart e1 "horizontalement",
e2 "verticalement", e3 en "profondeur" :

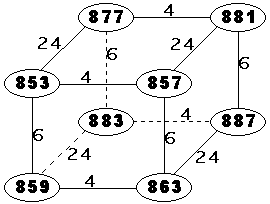
Ci-dessous le plus petit avec 8 nombres premiers consécutifs (e1=4,e2=6,e3=24) :

On peut aussi les représenter plus facilement sous la forme de suites symétriques des différences correspondantes caractéristique du type de la suite étudiée, avec le nombre premier de départ :

• "3D" : {13 ;4,2,4,14,4,2,4}
• "3D consécutifs" : {853 ;4,2,4,14,4,2,4}
  
  

Nombres premiers en réseau et k-uples :

On peut aussi les transformer en k-uples particuliers, par exemple:

• "2D Triangle consécutifs" : {4116419 + 0,24,30,48,54,60}
• "3D" : {13 + 0,4,6,10,24,28,30,34}
• "3D consécutifs" : {853 + 0,4,6,10,24,28,30,34}
  

Jumeaux en progression arithmétique (consécutifs) :

Si l'on considere le cas particulier e1=2, e2 croissant et les plus petits p1,p2,p3 correspondants, on obtient 3 nombres premiers impairs avec la plus petite différence (e1=2) et la plus grande (e2) , j'appelle ce triplet "nombres premiers écartelés":

Une étrange coïncidence apparait très souvent . Pour les e2 avec (*) on retouve les nombres pour la première occurence d'une différence de nombres premiers consécutifs ! N'y aurait-il pas une sorte de compensation immédiate entre un très petit et un très grand écart ?

Avec 2 jumeaux :

Avec 3 jumeaux :

Challenges :

Trouver des nombres premiers en réseau non consécutifs ou mieux, consécutifs (beaucoup plus difficile)

• Une chaîne de jumeaux la plus longue possible (*)
• Un reseau 2D du plus grand nombre de nombres premiers possible
• Un reseau 3D du plus grand nombre de nombres premiers possible
• ......

(*) Le 13 mai 2000 Paul Jobling a trouvé 12 chaines de 10 jumeaux en progression arithmétique non consécutifs :

i=0 à 9
(7146+i*7087)*17#+239670 +- 1
(27193+i*15352)*17#+39930 +- 1
(103299+i*8702)*17#+409602 +- 1
(240056+i*1185)*17#+399000 +- 1
(28070+i*24909)*17#+369168 +- 1
(43711+i*33725)*17#+160878 +- 1
(392688+i*2040)*17#+429018 +- 1
(263377+i*18202)*17#+359172 +- 1
(1952+i*70022)*17#+392772 +- 1
(104521+i*62645)*17#+353532 +- 1
(189110+i*89957)*17#+244200 +- 1
(419358+i*62769)*17#+424980 +- 1

•  Prime k-tuplets  de Tony Forbes.
•  Yves Gallot's Proth.exe and Cunningham Chains  de Warut Roonguthai.