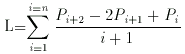Pi
ième nombre premier.
| n | L |
| 1 | 0.5 |
| 2 | 0.5 |
| 3 | 1 |
| 4 | 0.6 |
| 5 | 0.9333333333 |
| 6 | 0.6476190476 |
| 7 | 0.8976190476 |
| 8 | 1.1198412698 |
| 9 | 0.7198412698 |
| 10 | 1.0834776335 |
| 29 | 1.2586984668 |
| 102 | 1.0317178734 |
| 103 | 1.0030370602 |
| 104 | 1.0075100187 |
| 105 | 1.0072456589 |
| 106 | 1.0072096359 |
| 107 | 1.0071758495 |
Le minimum de L est pour n=1 ou 2 (p=2 ou 3) et le maximum semble être
pour n=29 (p=109), pour n<=104.
Cette valeur L se comporte comme a dans : 
Le 27 janvier 1999, Preda Mihailescu
démontre par transformation de la série que :
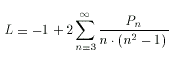
Sous cette forme il prouve la convergence de la série,
précise la valeur de L= 1.00717714..., et donne une estimation
de l'erreur sur la limite < 2/pi(n).
